Bruchzahlen verstehen
Mit den 8 flexiblen Interviews kann die Einsicht in Bruchzahlen und deren Darstellung mit Hilfe von geometrischen Modellen (Rechteck- und Würfelmodell) sowie dem Zahlenstrahl operativ erforscht werden. Es handelt sich um offene und erweiterbare Aufgaben, welche von den Studien von Piaget (1975) und Battista (1996, 1998) ausgehen. Sieben davon sind in Explorationsstudien an rund 200 Kindern (Durchschnittsalter 10;8 Jahre, Standardabweichung 3;5 Jahre) durch Studierende der HfH erprobt worden. Zum flexiblen Interview Nr. 3, Bruchzahlen und Zahlenstrahl, liegt eine Publikation vor, siehe Poster (Meyer, 2008).
Die Interviews können vom Kindergarten bis zur Sekundarstufe eingesetzt werden. Link zum Ueberblick.
Rollenspiele ermöglichen gute Einstiege in die Methode.
Organisieren Sie einladende Einzel- oder Gruppensituationen, in denen die Grundideen der Geometrie und der Arithmetik umgesetzt werden werden (vgl. Wittmann, 1999; Franke & Reinhold, 2016). Dabei treten die dialogische, operative Diagnostik in Wechselwirkungen mit der Denkschulung (vgl. Adey, 2008; Adey & Shayer, 1994).
Thema und didaktische Skizzen:
0 Bruchzahlen mit dem FI verstehen - Einleitung
1 Was ist ein Viertel? Würfelmodell
2 Was ist ein Viertel? Zeichne im Quadrat
3 Bruchzahlen und Zahlenstrahl - und Poster "number line and simple fractions" (Meyer, 2008)
4 Verdopple eineinhalb auf dem Zahlenstrahl
5 Quadratfläche von einem halben Meter Seitenlänge berechnen (Symbolisch)
6 Würfelvolumen vergleichen (Enaktiv)
7 Was ist ein Achtel? (Symbolisch am Würfelmodell)
8 Was ist ein Vierundsechzigstel (Symbolisch am Würfelmodell)
Der Kurzvortrag über Heinrich Winter (5:30 Min.) gibt eine mathematikdidaktische Einführung. Das flexible Interview unterstützt das entdeckende Lernen methodisch und erkenntnistheoretisch. Der Artikel von Gerald Wittmann (2006) "Grundvorstellungen zu Bruchzahlen – auch für leistungsschwache Schüler?" bietet wichtige Differenzierungen.
Die Erfahrungen mit der Didaktik des Bruchrechnens zeigen, dass es fragwürdig ist zu glauben, man könne Kindern die Einsicht in Bruchzahlen mit didaktischen Hilfsmitteln oder mit Regeln "spenden" (Christofidès-Henriques, 2003). Die flexiblen Interviews machen sichtbar, was die Kinder beim Denken und Darstellen verstehen und wie die Denkschulung weitergeführt werden könnte (vgl. Adey & Shayer, 1994; Adey, 2008). Die logisch-mathematische Analyse der Darstellungsmittel ist unabdingbar. Die flexiblen Interviews vertiefen die Einsichten in deren Verständnis. Weiter gilt: je wirkungsvoller und beziehungshaltiger der Geometrieunterricht ist, desto entwickelter sind die Zahlentheorien und Operationsverständnisse der Lernenden.
Wie sollte pädagogisch und fachdidaktisch vorgegangen werden, damit das Lehren und Lernen lebendig, interessengeleitet, produktiv, dynamisch und kognitiv anspruchsvoll erfahren werden kann? Wir stellen uns ein Labor vor, in dem Kinder, Jugendliche und auch Student*innen unter gezielter Führung die Bruchzahlen wiederentdecken können. Freudenthal (1991) bezeichnete das als "guided reinvention". Weitere theoretische Bezüge und Konzepte finden wir bei Lurija & Judowitsch (1982), sie sprachen vom pädagogischen Experiment; Steffe et. al. (2000) portraitierten das "experimental teaching"; Bell (1993a,b) hatte den Begriff des "diagnostic teaching" erläutert.
Die bewusste Integration des metakognitiven Denkens in die flexiblen Interviews eröffnet einen Prozess der "abstraction réfléchissante" (Piaget, 1977a, b) an. Adey & Shayer (1994) sowie Adey (2008) hatten diese Integration im Konzept der "Cognitive Acceleration" als Kombination bestehend aus den flexiblen Interviews und der Zone der nächsten Entwicklung (vgl. Wygotski, 1986) entwickelt und empirisch validiert. Die metakognitiven Fragen werden Schritt für Schrit in das bestehende Labor, Bruchzahlen verstehen, eingebaut. Unterstützung bei Experimenten und Übungen im Sinn der Lesson Study kann angefordert werden unter stefan.meyer[at]em.hfh.ch

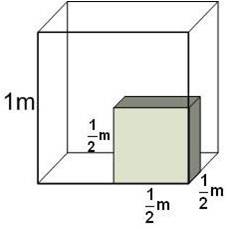 Ein Achtel (siehe FI 7)
Ein Achtel (siehe FI 7)